Содержание
Доклад и нанесение целей на карту (схему), ведение журнала наблюдения.
Умение быстро и правильно указывать обнаруженные цели, ориентиры и другие объекты на местности имеет важное значение для управления подразделением и огнем в бою. Целеуказание может производиться как непосредственно на местности, так и по карте или аэроснимку
При целеуказании соблюдаются следующие основные требования:
- местоположение целей указывать быстро, кратко, ясно и точно; цели указывать в строго установленном порядке, пользуясь принятыми единицами измерения;
- передающий и принимающий должны иметь общие ориентиры и твердо знать их расположение, иметь единое кодирование местности.
Целеуказание на местности осуществляется чаще всего от ориентира (местного предмета).
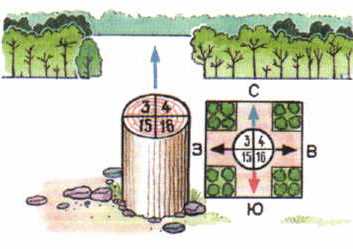
Целеуказание от ориентира (местного предмета) — наиболее распространенный способ целеуказания. При этом способе целеуказания вначале называют ближайший к цели ориентир (местный предмет), затем угол между направлением на ориентир (местный предмет) и направлением на цель в тысячных и удаление цели от ориентира (местного предмета) в метрах. Например: «Ориентир два, вправо сорок пять, дальше сто, у отдельного дерева — наблюдатель» или «Угол разрушенного дома, вправо двадцать, ближе сорок – пулемет».
Если передающий и принимающий цель имеют приборы наблюдения, то вместо удаления цели от ориентира (местного предмета) может указываться вертикальный угол между ориентиром и целью в тысячных. Например: «Ориентир четыре, влево тридцать, ниже десять — боевая машина в окопе» или «Угол разрушенного дома, вправо двадцать, ниже сорок – пулемет».
В некоторых случаях, особенно при выдаче целеуказания по малозаметным целям, используются только местные предметы, находящиеся вблизи цели. Например: «Ориентир два, вправо тридцать — отдельное дерево, дальше двести — развалины, влево двадцать, под кустом — пулемет».
⭐ Ориентирование по звездам
Звездное небо северного полушария
В северном полушарии стороны света определяются по созвездию Орион. Одна из звезд Ориона (Минтака) находится над небесным экватором и при восходе укажет точное направление на восток, при заходе соответственно на запад.
Звездное небо южного полушария
В южном полушарии находится созвездие Южный Крест. С его помощью определяют стороны света в этой части земли. Созвездие представляет собой четыре небесных тела, находящихся попарно друг против друга, напоминающие крест.
Линия, проведенная вдоль светил, образующих вертикальную часть креста, показывает направление север-юг. Юг находится в нижней части этой линии. Восток будет слева, запад – справа.
Ориентирование по полярной звезде
Пожалуй самый популярный способ ориентирования по астрономическим светилам. Он известен с древнейших времен. Основной навык здесь заключается в нахождении этой звезды на небесном своде. Полярная звезда всегда находится на севере.
Вначале находят созвездие Большой Медведицы. Это семь звезд, которые образуют большой ковш. Через две первых звезды большого ковша проводится прямая, длина которой равна пяти расстояния между взятыми звездами.
У края ручки малого ковша (малой медведицы) будет находится Полярная звезда. Направление взгляда на нее укажет где находится север, сзади будет юг, по левую руку – запад, по правую – восток.
Электромагнитный и лазерный дальномеры
Электромагнитный измеритель расстояния относится к так называемым приборам импульсного типа, точность их измерения считается средней и может иметь погрешность от 1,2 и до 2 метров. Но зато эти приборы имеют большое преимущество перед своими оптическими собратьями, так как оптимально подходят для определения расстояния между движущимися объектами. Единицы измерения расстояния у них могут исчисляться как метрами, так и километрами, поэтому их часто применяют при проведении аэрофотосъемки.
Что же касается лазерного дальномера, он предназначен для измерения не очень больших расстояний, обладает высокой точностью и очень компактен. Особенно это относится к современным портативным Эти устройства измеряют расстояние до объектов на расстоянии от 20-30 метров и до 200 метров, с погрешностью не более 2-2,5 мм на всей длине.
Простые способы определения и измерения расстояний на местности, глазомерный способ, по измеренным угловым величинам местных предметов, промером шагами, на слух.
Глазомерный способ — основной, самый простой и быстрый, наиболее доступный каждому в любых условиях. Однако точный глазомер приобретается не сразу. Он вырабатывается путем систематической тренировки, проводимой в разнообразных условиях местности, в различное время года и суток.
Чтобы развить свой глазомер, необходимо как можно чаще упражняться в определении на глаз расстояний с обязательной проверкой их шагами, по карте или другим способом. Тренировку надо начинать с коротких расстояний — 10, 50, 100 метров. Хорошо освоив эти дистанции, можно переходить последовательно к большим — 200, 400, 800, 1000 метров. Потом можно легко определять и большие расстояния.
На точность глазомерного способа указывают и влияют такие побочные явления, как:
— Более крупные предметы кажутся всегда ближе мелких, расположенных на том же расстоянии. — Чем меньше промежуточных предметов находится между глазом и наблюдаемым предметом, тем этот предмет кажется ближе. — При наблюдении снизу вверх, от подошвы горы к вершине, предметы кажутся ближе, а при наблюдении сверху вниз — дальше.
Глазомерная оценка расстояний может контролироваться, когда несколько человек измеряют одну и ту же дистанцию независимо друг от друга. Беря среднее из всех этих определений, получают наиболее точный замер. Для грубой оценки расстояний иногда пользуются примерными данными, приведенными в таблице ниже.
Каждый может уточнить и дополнить эту таблицу применительно к своим наблюдениям. Точность глазомерного способа зависит от натренированности наблюдателя, от величины определяемых расстояний и от условий наблюдения. Для расстояний до 1000 метров надо добиться тренировкой определения величин с ошибкой не более 10—15%.
Способ определения и измерения расстояний на местности парами шагов.
При измерении расстояний шагами надо натренироваться в ходьбе ровным шагом, особенно в неблагоприятных условиях. На подъемах и спусках, при движении по кочковатому лугу, в кустарнике и т. д. Кроме того, надо знать длину своего шага в метрах. Она определяется из промера шагами линии, длина которой известна заранее и должна быть не менее 200—300 метров.
При измерении расстояний шаги считают парами, обычно под левую ногу. После каждой сотни пар шагов счет начинается снова. Чтобы не сбиться со счета, полезно каждую пройденную сотню пар шагов отмечать на бумаге или же загибать последовательно пальцы рук, или любым другим способом. Ошибки определения расстояний шагами, при ровном хорошо выверенном шаге, в среднем достигают 2—4% измеренного расстояния.
Способ определения и измерения расстояний на местности по времени и скорости движения.
Определять расстояния можно по времени движения, если вы приблизительно знаете свою среднюю скорость движения. Так, например, если средняя скорость движения походным шагом равна 5 км/час, когда подъемы и спуски не более 5 градусов, то, пройдя 45 минут по времени, можно ориентировочно сказать, что вами пройдено 3,75 км.
Способ определения и измерения расстояний до стреляющих орудий.
Определение расстояний до стреляющих орудий основано на обнаружении, в момент выстрела, вспышки и образования дыма. Затем, зная, что скорость распространения звука в воздухе равна 330 м/сек, то есть округленно 1 км за 3 секунды, отсчитываем время в секундах от момента вспышки до момента слухового восприятия звука выстрела (или взрыва) и, поделив его на три, определяем расстояние до орудий в километрах.
При отсутствии часов отсчитывать секунды можно путем порядкового счета «про себя» двухзначных чисел (21, 22, 23, 24), начиная с момента вспышки от выстрела до прихода звука от нее. Отсчет каждого из этих чисел занимает примерно одну секунду. Навыки такого счета, соразмерного ходу секундной стрелки, довольно быстро приобретаются уже после 2— 3 тренировок в отсчете двухзначных чисел.
Способ определения и измерения расстояний на слух.
Ночью в условиях плохой видимости расстояния часто приходится оценивать на слух. Для этого надо уметь определять по характеру звуков их источники и знать, с каких примерно расстояний можно услышать эти звуки ночью. При нормальном слухе и благоприятных акустических условиях дальность слышимости можно приближенно считать такой, какой она дана в таблице ниже.
Эти данные меняются в зависимости от конкретных условий, в которых производится наблюдение. Поэтому должны учитываться каждым наблюдателем на основе его личного опыта.
По материалам книги «Карта и компас — мои друзья». Клименко А.И.
Измерение и построение дирекционных углов на карте. Переход от дирекционного угла к магнитному азимуту и обратно
На местности при помощи компаса (буссоли) измеряют магнитные азимуты направлений, от которых затем переходят к дирекционным углам.
На карте наоборот, измеряют дирекционные углы и от них переходят к магнитным азимутам направлений на местности.
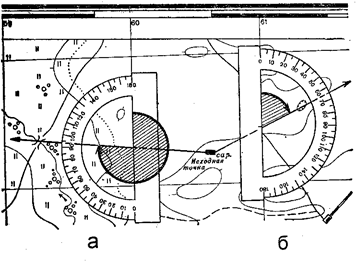Рис. 8. Изменение дирекционных угловна карте транспортиром
Дирекционные углы на карте измеряются транспортиром или хордоугломером.
Измерение дирекционных углов транспортиром производят в следующей последовательности:
- ориентир, на который измеряют дирекционный угол, соединяют прямой линией с точкой стояния так, чтобы эта прямая была больше радиуса транспортира и пересекала хотя бы одну вертикальную линию координатной сетки;
- совмещают центр транспортира с точкой пересечения, как показано на рис. 8 и отсчитывают по транспортиру значение дирекционного угла. В нашем примере дирекционный угол с точкой А на точку В равен 274° (рис. 8, а), а с точки А на точку С – 65° (рис. 8, б).
На практике часто возникает необходимость в определении магнитного АМ по известному дирекционному углу ά , или, наоборот, угла ά no известному магнитному азимуту.
Переход от дирекционного угла к магнитному азимуту и обратно
Переход от дирекционного угла к магнитному азимуту и обратно выполняют тогда, когда на местности необходимо с помощью компаса (буссоли) найти направление, дирекционный угол которого измерен по карте, или наоборот, когда на карту необходимо нанести направление, магнитный азимут которого измерен, на местности с помощью компаса.
Для решения этой задачи необходимо знать величину отклонения магнитного меридиана данной точки от вертикальной километровой линии. Эту величину называют поправкой направления (ПН).
Рис. 9. Схема магнитного склонения, сближения меридианов и поправка направления
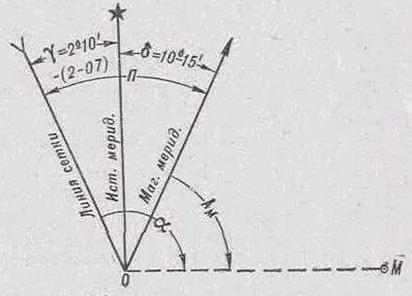Рис. 10. Определение поправки для перехода от дирекционного угла к магнитному азимуту и обратно
Поправка направления и составляющие ее углы — сближение меридианов и магнитное склонение указываются на карте под южной стороной рамки в виде схемы, имеющей вид, показанный на рис. 9.
Сближение меридианов (g) — угол между истинным меридианом точки и вертикальной километровой линией зависит от удаления этой точки от осевого меридиана зоны и может иметь значение от 0 до ±3°. На схеме показывают среднее для данного листа карты сближение меридианов.
Магнитное склонение (d) — угол между истинным и магнитным меридианами указан на схеме на год съемки (обновления) карты. В тексте, помещаемом рядом со схемой, приводятся сведения о направлении и величине годового изменения магнитного склонения.
Чтобы избежать ошибок в определении величины и знака поправки направления, рекомендуется следующий прием.
Из вершины углов на схеме (рис. 10) провести произвольное направление ОМ и обозначить дужками дирекционный угол ά и магнитный азимут Ам этого направления. Тогда сразу будет видно, каковы величина и знак поправки направления.
Если, например, ά = 97°12′, то Ам = 97°12′ — (2°10’+10°15′) = 84°47‘.
Способы измерения расстояний на местности
Метод отступов
Закрепляем начало длинной рулетки на одном конце базисной линии. Далее протягиваем рулетку по прямой, например, вдоль здания, к другому концу намеченной базисной линии и закрепляем ее там. Проверяем, чтобы она не провисала.
Другой, короткой рулеткой, протянутой под прямым углом измеряем боковые расстояния от базисной линии до отмеченных на плане объектов – деревьев и кустарников, технологических люков, колодцев, углов сооружений. При каждом измерении боковых расстояний отмечаем текущее значение базисной линии. Прямой угол задаем, используя любой большой прямоугольный объект, например кусок оргалита или фанеры. Кроме того, прямой угол можно задать с помощью «египетского» треугольника. Еще древним египтянам было известно, что в треугольнике, со сторонами 3, 4 и 5 м угол, лежащий напротив пятиметровой стороны — прямой угол 90°. Для удобства, вместо метров, можно использовать относительные величины, отрезки любого размера. Главное – соблюсти пропорции.
Этот метод измерений можно применять в любом месте участка, если предварительно обозначить базисную линию. Таким образом, двигаясь по базисной линии от начала длинной рулетки, снимаем показания в каждой точке, которая соотносится с объектами измерения.
На обмерном плане отмечаем исходную точку цифрой «0» , а направление измерений обозначаем стрелкой. Делая замеры, записываем значения одинаково, по линии, с которой они соотносятся, тогда потом их будет легче считывать.
Метод треугольника
Другим известным способом измерений является метод треугольника. В нем используется уже обозначенная базисная линия и рулетка. В этом методе замеры проводят от двух фиксированных точек на базисной линии.
На рисунке базисная линия проходит вдоль стены дома. В качестве фиксированных точек на базисной линии в этом случае удобно использовать углы дома. Для измерения, например, положения дерева на участке, измеряем расстояния между точками С и А, а далее между точками С и В. При переносе на рабочий план, циркулем проводим окружности с радиусами ас и вс. В месте пересечения окружностей будет вершина С – центр дерева.
Метод треугольника можно использовать для измерения любых элементов в саду. Метод особенно удобен для измерения объектов, непараллельных основному строению, находящихся под углом к нему. Это могут быть, например, дорожки или другие строения. Проводим измерения методом треугольника. В результате план может состоять из множества пересекающихся треугольников.
Сочетание этих двух методов позволяет проводить любые измерения расстояний на участке. Но есть еще один метод измерения расстояний на местности. Он не требует вообще никаких измерительных инструментов.
Измерение расстояний на местности шагами
Измерения расстояний шагами сводится к простому правилу: идя по измеряемому отрезку, считаем шаги. Удобно для подсчета использовать двузначные числа, потому что они по произношению «двусложные», например: «тридцать пять». Поэтому «тридцать» произносится под одну ногу, а «пять» — под другую. Таким образом, два шага — пара шагов будут соответствовать одному числу. К односложным числам можно добавлять протяжную букву «и», например: «и сорок». Это также будет соответствовать паре шагов.
Каждый человек, в одних и тех же условиях, имеет примерно одинаковую длину шага. Длину среднего шага можно принять равной одной четверти роста съемщика плюс 37 см. Так, если рост съемщика 1,72 м, то за среднюю длину его шага можно принять 43 см + 37 см = 80 см, а пара шагов равна 160 см. Чтобы получить более точное значение длины пары шагов, съемщик должен выверить их в тех условиях, в которых будут происходить измерения. Ошибка измерений такого метода, в среднем, не превышает 3% пройденного пути.
Другой, современный, способ измерения расстояний шагами, это использование фитнес браслета с шагомером или приложения шагомер на смартфоне. Здесь подсчеты и вычисления, описанные выше, происходят автоматически. Конечный результат смотрим на дисплее.
Измерение расстояний и определение площадей по топографической карте, численный, линейный и поперечный масштаб.
Чтобы произвести измерение расстояний потопографической карте, пользуются численным, линейным или поперечным масштабом. Расстояния между точками на топографической карте обычно измеряются циркулем-измерителем или курвиметром.
Численный масштаб топографической карты.
Это масштаб карты выраженный дробью, числитель которой – единица, а знаменатель – число, показывающее степень уменьшения на карте линий местности. Чем меньше знаменатель масштаба, тем крупнее масштаб карты. Подпись численного масштаба на картах обычно сопровождается указанием величины масштаба – расстояния на местности (в метрах или километрах), соответствующего одному сантиметру карты.
Например 1:50 000 – в 1 сантиметре 500 метров. Величина масштаба в метрах соответствует знаменателю численного масштаба без двух последних нулей. При определении расстояния с помощью численного масштаба линия на карте измеряетсялинейкой, полученный результат в сантиметрах умножается на величину масштаба.
Линейный масштаб топографической карты.
Линейный масштаб – графическое выражение численного масштаба. Он представляет собой прямую линию, разделенную на определенные части, которые сопровождаются подписями, означающими расстояния на местности.
Поперечный масштаб топографической карты.
Поперечный масштаб – график (обычно на металлической пластинке) для измерения и откладываниярасстояний на карте с предельной графической точностью (0,1 мм). Стандартный (нормальный) поперечный масштаб имеет большие деления, равные 2 см, и малые деления (слева на графике), равные 2 мм. Кроме того, на графике имеются отрезки между вертикальной и наклонной линиями, равные по первой горизонтальной линии 0,2 мм, по второй – 0,4 мм, по третьей – 0,6 мм и т. д.
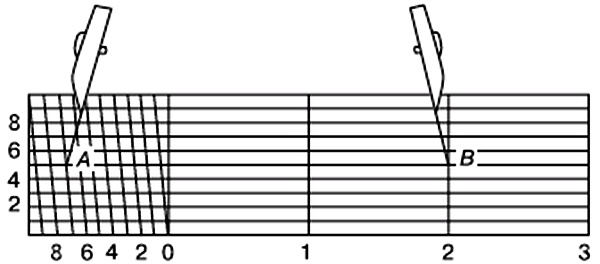
С помощью стандартного поперечного масштаба можно измерять и откладывать расстояния на карте любого (метрического) масштаба. Отсчет расстояния по поперечномумасштабу состоит из суммы отсчета на основании графика и отсчета отрезка между вертикальной и наклонной линиями. На рисунке выше, расстояние между точками А и В (при масштабе карты 1:100 000) равно 5500 метров (4 км + 1400 м + 100 м).
Измерение расстояний на карте циркулем–измерителем.
При измерении расстояния по прямой линии иглы циркуля устанавливают на конечные точки, затем, не изменяя раствора циркуля, по линейному или поперечному масштабу отсчитывают расстояние. В том случае, когда раствор циркуля превышает длину линейного или поперечного масштаба, целое число километров определяется по квадратамкоординатной сетки, а остаток – обычным порядком по масштабу.
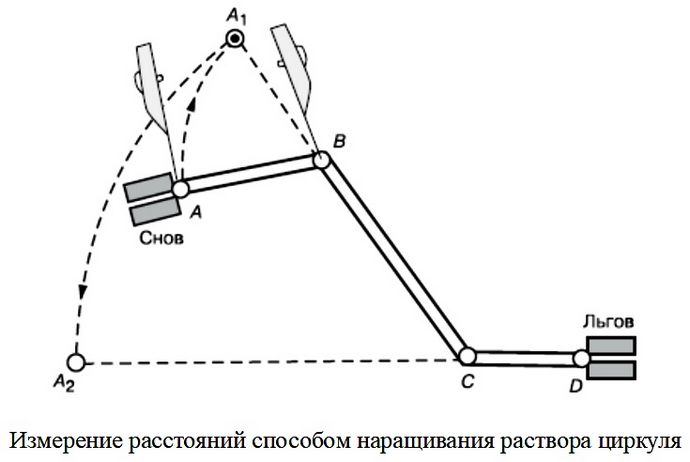
Измерение расстояний на карте шагом циркуля.
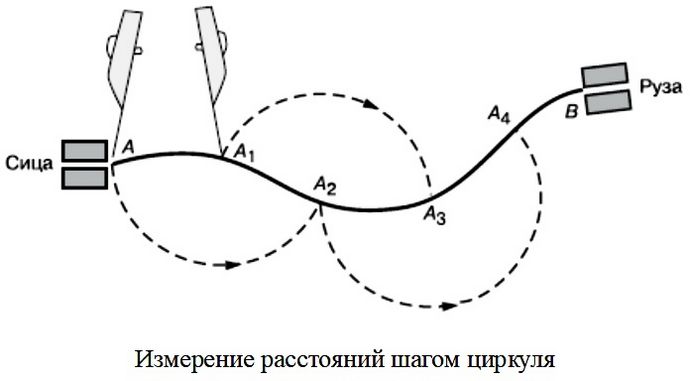
Ломаные линии удобно измерять путем последовательного наращивания раствора циркуля прямолинейными отрезками. Измерение расстояний и длин кривых линий производится последовательным отложением шага циркуля. Величина шага циркуля зависит от степени извилистости линии, но, как правило, не должна превышать 1 см. Для исключения систематической ошибки длину шага циркуля, определенную по масштабу или линейке, следует проверять измерением линии километровой сетки длиной 6–8 см.
Длина извилистой линии, измеренной по карте, всегда несколько меньше ее действительной длины, так как измеряются не кривая линия, а хорды отдельных участков этой кривой. Поэтому в результаты измерений покарте приходится вводить поправку – коэффициенты увеличения расстояний.
Измерение расстояний на карте курвиметром.
Вращением колесика стрелкукурвиметра устанавливают на нулевое деление, а затем прокатывают колесико по измеряемой линии с равномерным нажимом слева направо или снизу вверх. Полученный отсчет в сантиметрах умножают на величину масштаба данной карты.
Определение расстояний по прямоугольным координатам точек.
Определение расстояний попрямоугольным координатам точек в пределах одной зоны карты можно произвести по формуле
где D – длина линии, x1, y1 – координаты начальной точки прямой, x2, y2 – координаты конечной точки прямой.
Определение площадей по квадратам километровой сетки карты.
Площадь участка определяется подсчетом целых квадратов и их долей, оцениваемых на глаз. Каждому квадрату километровой сетки соответствует: на картах масштаба 1:25 000 и 1:50 000 – 1 км2, на картах масштаба 1:100 000 – 4 км2, на картах масштаба 1:200 000 – 16 км2.
По материалам книги Способы автономного выживания человека в природе.Под редакцией Л. А. Михайлова.
Измерение расстояний на местности дистанционно
В случае нахождения объекта измерения в зоне прямой видимости, но при наличии неодолимой преграды, делающей невозможным прямой доступ к объекту, (например озера, речки, болота, ущелья и пр), применяется измерение расстояния дистанционно визуальным методом, а точнее методами, так как существует их несколько разновидностей:
- Высокоточные измерения.
- Низкоточные или приблизительные измерения.
К первым относятся измерения при помощи специальных приборов, таких, как оптические дальномеры, электромагнитные или радиодальномеры, световые или лазерные дальномеры, ультразвуковые дальномеры. Ко второму виду измерений относится такой способ, как геометрический глазомерный. Тут и определение расстояния по угловой величине предметов, и построение равных прямоугольных треугольников, и метод прямой засечки многими другими геометрическими способами. Рассмотрим некоторые из способов высокоточных и приблизительных измерений.
Варианты определения расстояний до объектов
Среди полезных умений, которые рекомендуется освоить всем, кто предпочитает спокойному отдыху активный, относится определение расстояния на местности. Ситуаций, когда этот навык может пригодиться, множество – отсутствие картографического материала или его порча, утеря, необходимость определить ширину реки на глаз, расстояние до цели, произвести расчет высоты дерева, которое нужно использовать в качестве моста и другое.
Существует не один способ определения расстояний на местности
Существующие варианты отличаются различной погрешностью измерений и инструментарием. Узнать расстояние можно:
- Методом «на глаз». Подходит, когда на местности есть признаки цивилизации, хотя бы столбы связи.
- С помощью собственных шагов. Это удобный способ вычисления длины маршрута. Поскольку длина шага – величина постоянная, рекомендуется заранее ее узнать и запомнить.
- По видимости объектов. Требует навыка, дает наиболее точный результат в ясную погоду.
Способ определения расстояния по степени видимости и кажущейся величине цели
Известно, что любой предмет с разных дистанций виден по-разному. На близком расстоянии видны мелкие детали. Затем, по мере удаления предмета, они как бы стираются, и можно различать лишь более крупные детали. Наконец, и крупные детали стираются, остается видимым лишь общий контур предмета. Эти три этапа видимости предметов имеют свои, так называемые промежуточные рубежи, на которых видны какие-либо характерные детали предмета, а другие не различимы. Отсюда — определенная закономерность степени видимости предмета на разных расстояниях.
Зная эту закономерность видимости каждого предмета, стрелок может точно определить расстояние до него.
Конкурс Измерение расстояния
Определение расстояния до предмета
1. Измерение расстояния и с помощью большого пальца.Этот способ удобно применять в том случае, когда предмет движется мимо наблюдателя, но он пригоден и для определения дальности неподвижных предметов.
Допустим, что надо измерить расстояние до пешехода. В этом случае следует вытянуть вперёд руку с поднятым большим пальцем и закрыть один глаз (правый глаз закрывается тогда, когда пешеход движется справа налево). В тот момент, когда пешеход покроется пальцем (рис.1), нужно закрыть левый глаз и открыть правый. Пешеход при этом покажется отодвинутым назад(рис.2)
Теперь нужно сосчитать, сколько шагов успеет сделать пешеход до того момента, когда он снова покроется пальцем. Расстояние до пешехода будет равняться числу шагов, умноженному 10. Предположим, что он успел сделать 16 шагов: 16×10=160 шагов. Если при этом считать, что шаг человека равен в среднем 0,75 м, то до пешехода 120 м.
2. Определение расстояния при помощи измерения углов. Этот способ сложнее и требует некоторой тренировки. Исходным положением для измерения расстояний этим способом является следующее правило: каждый предмет, видимый под углом в 1º, удалён на расстояние в 57 раз больше своего поперечника. Предмет, видимый под углом в 2°, удален на 28 поперечников; под углом в 5° — на 11 поперечников; под углом в 7° — на 8 поперечников и т, д. Если известен угол, под которым виден предмет, можно приблизительно определить и расстояние до него. Простейший способ измерения — с помощью указательного пальца. Нужно вытянуть руку и поднять указательный палец (расстояние от пальца до глаз берется за 60 см). Предмет, который покрывается ногтем указательного пальца (ширина ногтя 1 см), обычно виден под углом в 1° и находится на расстоянии в 57 раз больше своего поперечника. Если ноготь покрывает лишь половину предмета, значит, угловая его величина 2°, а расстояние до него равно 28 его поперечникам. Для измерений можно пользоваться ногтевым суставом большого пальца. Его длина обычно 3,5 см. Предмет, который покрывается этим суставом при вытянутой руке, виден примерно под углом в 3° и удалён на расстояние в 18 раз больше своего поперечника.
Определение ширины водоёмов
1. Нужно подойти как можно ближе к воде и заметить на противоположном берегу два каких-либо предмета, расположенных у самой кромки воды. Затем нужно взять травинку (палочку, бечёвку) и, держа её горизонтально за концы обеими вытянутыми руками, закрыть один глаз. Глядя поверх травинки, надо закрыть ею промежуток между замеченными ориентирами. После этого следует отметить точку, в которой вы находитесь, сложить травинку пополам и отойти от водоёма под прямым углом до другой точки, из которой расстояние между ориентирами закроется укороченной травинкой. Расстояние от этой точки до реки, где вы производили измерение в первый раз, и будет равно ширине водоёма.
2. Нужно подойти к воде, засечь на противоположном берегу какой-либо ясно видимый предмет А, расположенный у самой кромки воды, и отметить точку своего стояния камнем или колышком Б. Затем нужно пройти вдоль берега по линии, перпендикулярной к направлению между А и Б, ровно 30 шагов, воткнуть палку В, отс
